4.6 Conditional Probability Lesson 06

Here the first event will affect the second one. Figure 1 shows an example of it.

Figure 1

Figure 1

Figure 1 - Example of conditional probability.

The first event is to determine the bird type, and the second event the probability to run on the morning. Have in mind, these two birds has different probability to run on the morning.

  • The early bird has 0.02;
  • The night owl has 0.00.

4.6.1 Medical Example

Supose a patient with a disease, the probability of this patient has cancer is 0.9 and to be free cancer is 0.1.

\[P(cancer) = 0.1 \\ P(\neg \ cancer) = 0.9 \tag{1}\]

To be honest, we do not know if this patient has cancer, so it is necessary to apply a test. This test is not perfect, it means, there are a probability to indicates a false positive and a false negative.

For this reason, I introduce the conditional probability.

\[ P(Positive | cancer) = 0.9 \tag{2}\]

What is the meaning of this notation?

Given the patient has cancer, the probability of this test indicates positive is 0.9. Thus, given the patient has cancer and the test indicates negative is 0.1, as shown in equation (3).

\[ P(Negative | cancer) = 0.1 \tag{3}\]

Analogous to the case of the patient do not has cancer.

\[ P(Positive | \neg \ cancer) = 0.2 \\ P(Negative | \neg \ cancer) = 0.8 \tag{2} \]

Table 1 shows a representation in a tabular way.

Table 1 - Truth Table for Medical Example
Disease Test \(P_{disease}\) \(P_{test}\) P Q1: Test Positive? Q1: Answer
No Negative \(P(\neg \ cancer) = 0.9\) \(P(Negative\|\neg \ cancer) = 0.8\) 0.72 No 0
No Positive \(P(\neg \ cancer) = 0.9\) \(P(Positive\|\neg \ cancer) = 0.2\) 0.18 Yes 0.18
Yes Negative \(P(cancer) = 0.1\) \(P(Negative\| cancer) = 0.1\) 0.01 No 0
Yes Positive \(P(cancer) = 0.1\) \(P(Positive\| cancer) = 0.9\) 0.09 Yes 0.09
\(\sum = 1\) \(\sum = 0.27\)

What is the probability the test is positive?

Q1: 0.27

4.6.1.1 Coin flip example

Two coins, one fair and other loaded.

  • Coin 1: \(P_1(HEADS) = P_1(TAILS) = 0.5\);
  • Coin 2: \(P_2(HEADS) = 0.9\) and \(P_2(TAILS) = 0.1\).
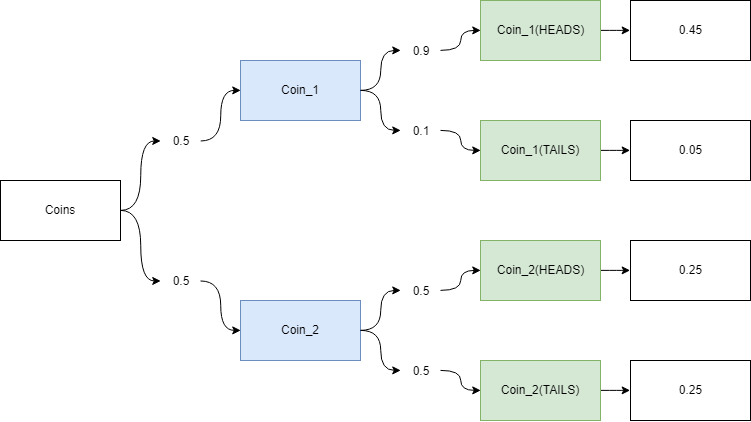
Figure 2

Figure 2

Figure 2 - Coin Example of conditional probability.

What is the probability of this sequence HEADS and TAILS?

Coin Flip 1 Flip 2 \(P_{coin}\) \(P_{Flip 1}\) \(P_{Flip 2}\) P Q2: HEADS then TAILS? Q2: answer
1 H H 0.5 0.9 0.9 0.405 No 0
1 H T 0.5 0.9 0.1 0.045 Yes 0.045
1 T H 0.5 0.1 0.9 0.045 No 0
1 T T 0.5 0.1 0.1 0.005 No 0
2 H H 0.5 0.5 0.5 0.125 No 0
2 H T 0.5 0.5 0.5 0.125 Yes 0.125
2 T H 0.5 0.5 0.5 0.125 No 0
2 T T 0.5 0.5 0.5 0.125 No 0
\(\sum = 1\) \(\sum = 0.170\)

4.6.1.2 Summary

In this lesson you learned about conditional probability. Often events are not independent like with coin flips and dice rolling. Instead, the outcome of one event depends on an earlier event.

For example, the probability of obtaining a positive test result is dependent on whether or not you have a particular condition. If you have a condition, it is more likely that a test result is positive. We can formulate conditional probabilities for any two events in the following way:

  • \(P(A|B) = \frac{P(A\text{ }\cap\text{ }B)}{P(B)}\)
  • \(P(A ∩ B)\)

In this case, we could have this as:

\[P(positive|disease) = \frac{P(\text{positive }\cap\text{ disease})}{P(disease)}\]

where ∣ represents “given” and \(\cap\) represents “and”. — Class notes - Text: Summary

 

A work by AH Uyekita

anderson.uyekita[at]gmail.com