4.7 Bayes Rule Lesson 07
The person who writes down this theorem.
Thomas Bayes (/beɪz/; c. 1701 – 7 April 1761) was an English statistician, philosopher and Presbyterian minister who is known for formulating a specific case of the theorem that bears his name: Bayes’ theorem. Bayes never published what would become his most famous accomplishment; his notes were edited and published after his death by Richard Price. — Wikipedia - Thomas Bayes
4.7.1 Cancer Example
The probability to a person has cancer is 1% and the probability to the test gives positive is 90%. If a person do not has cancer the probability of the test gives negative is 90%.
What is the probability of a given positive test the person has cancer?
| Disease | Test | \(P_{disease}\) | \(P_{test}\) | P | Q1: Test positive? | Q1: answer |
|---|---|---|---|---|---|---|
| No | Negative | 0.99 | 0.90 | 0.891 | No | 0 |
| No | Positive | 0.99 | 0.10 | 0.099 | Yes | 0.099 |
| Yes | Negative | 0.01 | 0.10 | 0.001 | No | 0 |
| Yes | Positive | 0.01 | 0.90 | 0.009 | Yes | 0.009 |
| SUM = 0.108 |
Bear in mind, the probability of a false positive is 0.099, which is 11 times bigger than the a truth valeu of 0.009.
Figure 1 ilustrate this situation.
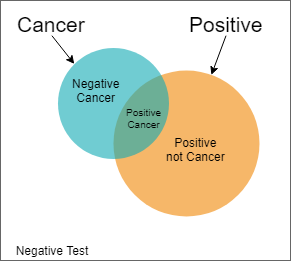
Given the test is positive, the probability of this person has cancer is:
\[ P(C\|Positive) = \frac{P(C,Positive)}{P(C,Positive) + P(\neg \ C,Positive)} = \frac{0.009}{0.009 + 0.099} = 0.08333\]
4.7.2 Bayes Rule
From the example above, I can point out some definitions:
Prior:
This is a information before the test.
\[ P(C) = 0.01 \\ P(\neg C) = 0.99 \tag{1}\]
Joint:
Now, I will apply the test for a given positive result.
\[ P(C,Positive) = P(C) * \underbrace{P(Positive\|C)}_{Sensibility} \\ P(\neg C,Positive) = P(\neg \ C) * \underbrace{P(Positive\| \neg \ C)}_{Sensibility} \tag{2} \]
For a negative result.
\[ P(C,Negative) = P(C) * \underbrace{P(Negative\|C)}_{Specitivity} \\ P(\neg \ C,Negative) = P(\neg \ C) * \underbrace{P(Negative\| \neg \ C)}_{Specitivity} \tag{3}\]
Normalization:
This is performed for each result (Positive and Negative).
\[ P(Positive) = P(C,Positive) + P(\neg \ C,Positive) \tag{4}\]
Posterior:
Divide the \(P(C,Positive)\) and \(P(\neg C,Positive)\) by \(P(Positive)\).
\[P(C|Positive) = \frac{P(C,Positive)}{P(Positive)} \tag{5}\]
\[P(\neg C|Positive) = \frac{P(\neg C,Positive)}{P(Positive)} \tag{6}\]
Finally, the Bayes equation could be generalized as:
\[P(A|B) = \frac{P(A) * P(B|A)}{P(B)} \tag{7}\]
A work by AH Uyekita
anderson.uyekita[at]gmail.com